关于“验证牛顿第二定律实验”的两个系统误差及修正
江苏省洪泽中学 陈正海
【摘 要】 通过改进实验装置,简化实验过程,消去原装置所内生的系统误差。
【关键词】 系统误差 误差分析
“探究加速度与力、质量的关系”实验是高中物理的一个重要实验,有利于学生理解、掌握物理方法:控制变量法;抓住主要矛盾法(M车?m);作图法(抽象问题形象化),有利于学生研究性学习和创新能力的培养。本文就实验装置内生的系统误差作出理论分析,并通过装置的改进对实验进行适度研究。
苏教版“验证牛顿第二定律实验”采用如下实验装置:
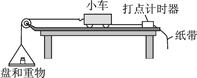
用上述实验装置实验时明确要示:1. 实验时首先要平衡摩擦力;2.小车包括砝码的质量要远大于砂和砂桶的总质量。这都是为什么呢?有无改进的装置,无需平衡摩擦力和小车包括砝码的质量要远大于盘和重物的总质量呢?本文就上述两个问题作简单的论述。
要求1:在利用打点计时器和小车做“验证牛顿第二定律”的实验时,实验首先要平衡摩擦力。
分析1:牛顿第二定律表达式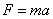 中的F是物体所受的合外力,在本实验中如果不采用一定的办法平衡小车及纸带所受的摩擦力,小车所受的合外力就不只是细绳的拉力,而应是细绳的拉力和系统所受的摩擦力的合力.因此,在研究加速度a和外力F的关系时,若不计摩擦力,误差较大,若计摩擦力,其大小的测量又很困难;在研究加速度a和质量m的关系时,由于随着小车上的砝码增加,小车与木板间的摩擦力会增大,小车所受的合外力就会变化(此时长板是水平放置的),不满足合外力恒定的实验条件,因此实验前必须平衡摩擦力。
中的F是物体所受的合外力,在本实验中如果不采用一定的办法平衡小车及纸带所受的摩擦力,小车所受的合外力就不只是细绳的拉力,而应是细绳的拉力和系统所受的摩擦力的合力.因此,在研究加速度a和外力F的关系时,若不计摩擦力,误差较大,若计摩擦力,其大小的测量又很困难;在研究加速度a和质量m的关系时,由于随着小车上的砝码增加,小车与木板间的摩擦力会增大,小车所受的合外力就会变化(此时长板是水平放置的),不满足合外力恒定的实验条件,因此实验前必须平衡摩擦力。
由于在实验开始以后,阻碍小车运动的阻力不只是小车受到的摩擦力,还有打点计时器限位孔对纸带的摩擦力及打点时振针对纸带的阻力.所以平衡摩擦力可采用下面的做法:将长木板的末端垫高一些,给小车一个沿斜面向下的初速度,使小车沿斜面向下运动.取下纸带后,如果在纸带上打出的点子的间隔基本上均匀,就表明小车受到的阻力跟它的重力沿斜面的分力平衡.为什么点子的间隔只能是基本上均匀呢?这是因为打点计时器工作时,振针对纸带的阻力是周期性变化的,所以难以做到重力沿斜面方向的分力与阻力始终完全平衡,小车的运动不是严格的匀速直线运动,纸带上的点子间隔也不可能完全均匀,所以上面提到要求基本均匀。
改进1:可以通过气垫导轨来减少摩擦;用位移传感器来削去振针对纸带的周期性阻力,保证物体在运动时受动的是恒力作用。
气垫导轨利用小型气源将压缩空气送入导轨内腔。空气再由导轨表面上的小孔中喷出,在导轨表面与滑行器内表面之间形成很薄的气垫层。滑行器就浮在气垫层上,与轨面脱离接触,因而能在轨面上做近似无阻力的直线运动,极大地减小了由于摩擦力引起的误差。使实验结果接近理论值。
位移传感器又称为线性传感器,通过电位器元件将机械位移转换成与之成线性或任意函数关系的电阻或电压输出。可以避免振针对纸带周期性的阻力,使物体在恒力作用下运动。
要求2. 在“验证牛顿第二定律”的实验中,小车包括砝码的质量要远大于盘和重物的总质量。
分析2:因为本实验是验证牛顿第二定律,在实验中物体m是被研究的对象,而不能把M和m看成一个整体,实验中物体M只是起到一个使物体m产生一个合外力的作用,并不能把M当作研究的对象。根据牛顿第二定律的表达式F=ma ,其中m就是被研究对象的质量。
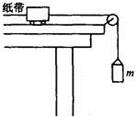 如图所示:在做
如图所示:在做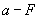 关系实验时,用盘和重物的重力
关系实验时,用盘和重物的重力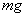 代替小车所受的拉力F,
代替小车所受的拉力F,
 而砂和砂桶的重力
而砂和砂桶的重力 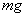 与小车所受的拉力 F是并不相等.这是产生实验系统误差的原因,为此,必须根据牛顿第二定律分析
与小车所受的拉力 F是并不相等.这是产生实验系统误差的原因,为此,必须根据牛顿第二定律分析 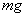 和 F在产生加速度问题上存在的差别.实验时可得到加速度与力的关系的图像。
和 F在产生加速度问题上存在的差别.实验时可得到加速度与力的关系的图像。 设小车实际加速度为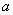 ,由牛顿第二定律可得:
,由牛顿第二定律可得: 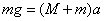 即
即 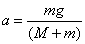
在近似处理时,用砂和砂桶的重力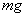 替代小车所受的拉力F,,则
替代小车所受的拉力F,,则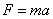 ,近似为mg = Ma设这种情况下小车的加速度为
,近似为mg = Ma设这种情况下小车的加速度为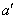 ,则
,则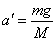 .在本实验中,M保持不变,与
.在本实验中,M保持不变,与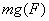 成正比,而实际加速度
成正比,而实际加速度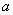 与
与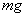 成非线性关系,且
成非线性关系,且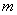 越大,图像斜率越小。理想情况下,加速度
越大,图像斜率越小。理想情况下,加速度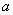 与实际加速度
与实际加速度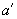 差值为
差值为

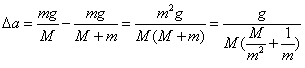
上式可见,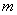 取不同值,
取不同值,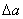 不同,
不同,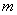 越大,
越大,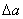 越大,当时m<<M,
越大,当时m<<M,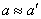 ,
,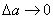 ,这就是要求该实验必须满足m<<M,的原因所在.
,这就是要求该实验必须满足m<<M,的原因所在.
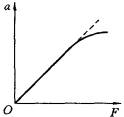
由图还可以看出,随着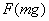 的增大,加速度的实验值与理想值之间的差别越来越大.
的增大,加速度的实验值与理想值之间的差别越来越大.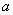 =g 是实验值(实线)的渐进线。
=g 是实验值(实线)的渐进线。
本实验是因原理不完善引起的系统误差,实验用砂和砂桶的总重力mg代替小车的拉力,而实际小车所受的拉力要小于砂和砂桶的总重力,这个砂和砂桶的总质量越接近小车和砝码的总质量,误差越大,反之砂和砂桶的总质量越小于小车和砝码的总质量,由此引起的误差就越小。但即使m<<M,仍不可能消去此系统误差。
改进2:可以引入力传感器来消去这个系统误差。力传感器,它的弹性敏感元件为一端封闭的薄壁圆筒,其另一端带有法兰与被测系统连接。当力作用于内腔时,圆筒变形成“腰鼓形”,使电桥失去平衡,输出与压力成一定关系的电压。可以直接读出力的大小。从而不再用砂和砂桶的总重力mg来代替小车的拉力,消去系统误差。
通过改进后我们采用如下的实验装置。

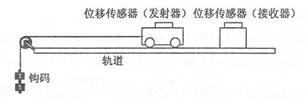
力传感器的引入可以直接读出绳子的张力,从而削去第一个系统误差,气垫导轨和位移传感器的引入可以不用再平衡摩擦力,另外使物体受到恒力作用,减少从第二个误差。
【参考文献】
刘炳升 物理实验教学多元创新中的几个关系问题 物理教学 201105
王欣 物理科学方法教育的理论与实践 陕西人民教育出版社 1988
李娟 验证牛顿第二定律实验中的三个为什么? 中学物理 2013.03
第二篇:系统的牛顿第二定律及应用
系统的牛顿第二定律及应用
一、系统的牛顿第二定律
若将系统受到的每一个外力,系统内每一物体的加速度均沿正交坐标系的x轴与y轴分解,则系统的牛顿第二定律的数学表达式如下:
F1x+F2x+…=m1a1x+m2a2x+…
F1y+F2y+…=m1a1y+m2a2y+…
与采用隔离法、分别对每一物体应用牛顿第二定律求解不同的是,应用系统的牛顿第二定律解题时将使得系统内物体间的相互作用力变成内力,因而可以减少不必求解的物理量的个数,导致所列方程数减少,从而达到简化求解的目的,并能给人以一种赏心悦目的感觉,现通过实例分析与求解,说明系统的牛顿第二定律的具体应用,并力图帮助大家领略到应用系统的牛顿第二定律求解的优势。
二、系统的牛顿第二定律的应用
1、求系统所受到的外力
例1 在图1中,A为电磁铁,C为胶木秤盘,A和C(包括支架)的总质量为M。B为铁片,质量为m。整个装置用轻绳悬挂于O点。当电磁铁通电,铁片被吸引上升的过程,轻绳上的拉力F的大小为( )
A、F=Mg
B、Mg<F<(m+M)g
C、F=(m+M)g
D、F>(m+M)g
分析与解 以A、B、C系统为研究对象,它受到的外力为竖直向下的重力(m+M)g,绳对系统竖直向上的拉力F(电磁铁A与铁片B间的相互引力为内力)。A、C的加速度为0,铁片上升时向上的加速度不为0。若以竖直向上方向为正向,设某时刻铁片B向上的加速度为a,则由系统的牛顿第二定律得
F-(m+M)g=ma
∴F=(m+M)g+ma>(m+M)g
因此,应选正确答案D。
例2 如图2所8示,一根长为l的轻杆,两端各固定一个质量均为m的小球A和B。若轻杆以它的中点O为轴在竖直平面内转动,求轻杆转到竖直位置时,杆对轴的作用力。
分析与解 取小球A、B及杆为研究对象,它受到竖直向下的重力2mg,轴对它竖直向上的弹力N.A、B在最低点与最高点时向心加速度恰为反向。若取竖直向上方向为正向,由系统的牛顿第二定律得:
N-2mg=maA+maB
∵aA=-aB ∴N=2mg
由牛顿第三定律知杆对轴的弹力大小为2mg,方向竖直向下。
由此题的解答不难知道,杆转到任意位置时对轴的压力大小均为2mg。
例3 如图3所示,质量为mC倾角为θ的斜面体C置于粗糙水平上。质量分别为mA、mB的A、B物体通过不可伸长的轻绳连接后将A置于斜面上,而B则通过固定在斜面顶端的轻定滑轮竖直悬挂起来。当A沿斜面以大小为a的加速度匀加速上升时,斜面体C始终静止不动。求此过程中地面对斜面体施加的支持力与摩擦力。
分析与解 取A、B、C及绳为研究对象,它受到的外力是竖直向下的重力(mA+mB+mC)g,地面竖直向上的支持力N及水平方向的静摩擦力f。将A物体的加速度沿水平方向与竖直方向分解,如图4所示,对系统在水平方向上应用牛顿第二定律得
f=mAa1=mAacosθ
摩擦力的方向与a1方向相同,即水平向右。
若取竖直向上方向为正向,对系统在竖直方向应用牛顿第二定律得
N-(mA+mB+mB)g=mAa2-mBa
∴N=(mA+mB+mC)g+mAasinθ-mBa
2、求加速度
例4 如图5所示,在光滑的绝缘水平面上固定着三个等质量的带电小球A、B、C,三球排成一直线。若释放A球瞬间(其它两球仍固定),它的加速度大小为2m/s2,方向向右;若释放B球瞬间(其它两球仍固定),它的加速度大小为4m/s2,方向向左,现只释放C球,求它的加速度。
分析与解 分别释放A、B、C三球时,每球产生加速度的原因是另两球对它的库仑力所致。若同时释放三球,则在释放瞬间由于每一球的受力情况与分别释放三球时的受力情况相同,因此每球的加速度不变,而对A、B、C三球构成的系统,三球同时释放时所受合外力为零。由系统的牛顿第二定律得0=maA+maB+maC
若取向右方向为正向,则aA=2m/s2,aB=-4m/s2.将加速度代放上式解得aC=2m/s2表明C球的加速度大小为2m/s2,方向向右。
例5 如图6所示,一根轻绳跨过轻质定滑轮,一端接一质量为M的物体,另一端吊一载人的梯子而处于静止,其中人的质量为m。为使滑轮对天花板的作用力为0,人在梯子上应如何运动?
分析与解 当悬吊重物的绳中张力为0时,滑轮对天花板无作用力,因此重物必定以a1=g的加速度加速下落,梯子则以a2=g的加速度上升,若取重物、梯子、人为研究对象,所受合外力为2Mg。取向下方向为正向,设人的加速度为a,则由系统的牛顿第二定律得2Mg=ma+Mg-(M-m)g
∴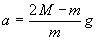 (人以此加速度下落)。
(人以此加速度下落)。
例6 质量为M的机车拉着质量为m的车厢在平直轨道上以加速度a做匀速运动。当速度为v时,车厢与机车脱钩,此后机车以加速度a1继续做匀加速运动(牵引力不变),求车厢在停止运动前所走的路程。
分析与解 以机车与车厢为研究对象,脱钩前后,系统受到的合外力未变(变化的只是系统内部的弹力),因此可应用系统的牛顿第二定律先求出脱钩后车厢的加速度,再运用运动学公式即可求出车厢停止运动前所走的路程。
以机车的加速度方向为正向,设车厢脱钩后的加速度为a2,系统所受的合外力为F,则对脱钩前后分别应用牛顿第二定律得F=(m+M)a,F=Ma1+ma2
由以上两式解得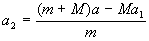
由运动学公式 vt2=v02+2as得
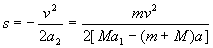
上述例举的问题,也可采用隔离法,分别对每一个物体应用牛顿第二定律列式求解。